Los cubos perfectos es el resultado de multiplicar un número entero tres veces. Este concepto tiene un significado especial en matemáticas. Representa una forma de expresar cantidades que se relacionan con el volumen y la estructura de figuras tridimensionales. Los cubos perfectos no solo son útiles en el estudio de la aritmética, tienen aplicaciones en el álgebra y en problemas de la vida cotidiana donde se necesita calcular volúmenes o explorar patrones numéricos.
Propiedades de los cubos perfectos
Los cubos perfectos son valores que se obtienen al multiplicar un número entero tres veces. Representan una forma especial de número que tiene propiedades únicas en matemáticas. Ejemplos los cubos perfectos se caracterizan al crecer rápidamente y están estrechamente relacionados con la geometría y que pueden visualizarse, volúmenes de cubos tridimensionales.
- Propiedades de los cubos perfectos
- Resultado de elevar un entero al cubo:
- Un cubo perfecto siempre proviene de un número entero elevado a la potencia.
- Crecimiento rápido:
- A medida que los números enteros aumentan, los cubos perfectos crecen rápidamente.
- Ejemplo 1³ = 1,2³ = 8,10³ =1000
- A medida que los números enteros aumentan, los cubos perfectos crecen rápidamente.
- Paridad:
- El cubo perfecto de un número par es siempre par 4³=64.
- El cubo perfecto de un número impar es siempre impar 3³=27.
- Resultado de elevar un entero al cubo:
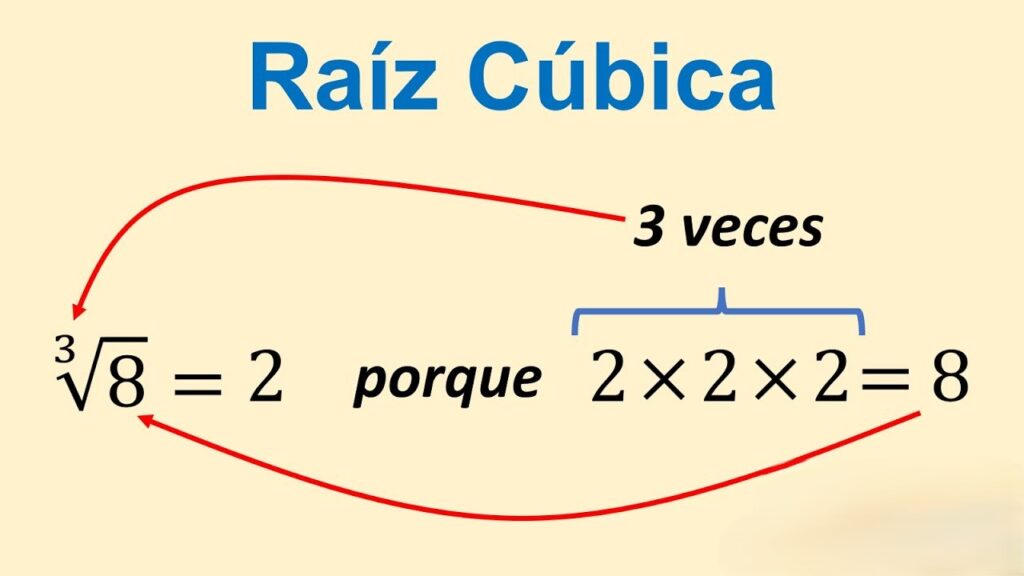
- Propiedad de las raíces cúbicas
- Todo cubo perfecto tiene una raíz cúbica exacta que es un número entero.
- Ejemplo: La raíz cúbica de 27 es 3
- Todo cubo perfecto tiene una raíz cúbica exacta que es un número entero.
- Relación con los factores primos
- Simetría en los dígitos terminales
- Los cubos perfectos tienen ciertos patrones en los dígitos finales.
- Ejemplo: 2³ = 8, 12³ =1728 terminan en 8.
- Los cubos perfectos tienen ciertos patrones en los dígitos finales.
- Diferencia entre dos cubos consecutivos
- La diferencia entre los cubos de dos enteros consecutivos aumenta con el tamaño de los números.
- 2³ −1³ =8−1=7,
- 3³ – 2³ = 27 – 8 =19.
- La diferencia entre los cubos de dos enteros consecutivos aumenta con el tamaño de los números.
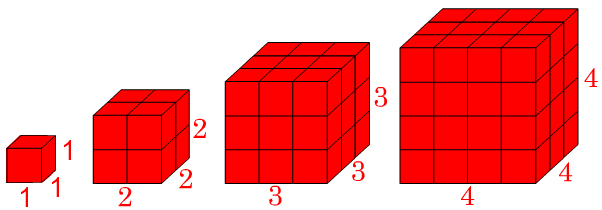
- Geometría
- Representan el volumen de un cubo geométrico cuyo lado tiene una longitud igual al número base.
- Ejemplo: Un cubo con lado de 3 tiene un volumen de 3³ =27
- Representan el volumen de un cubo geométrico cuyo lado tiene una longitud igual al número base.
- Aplicaciones prácticas
- Se usan en problemas de volumen, ingeniería, computación y análisis matemático.
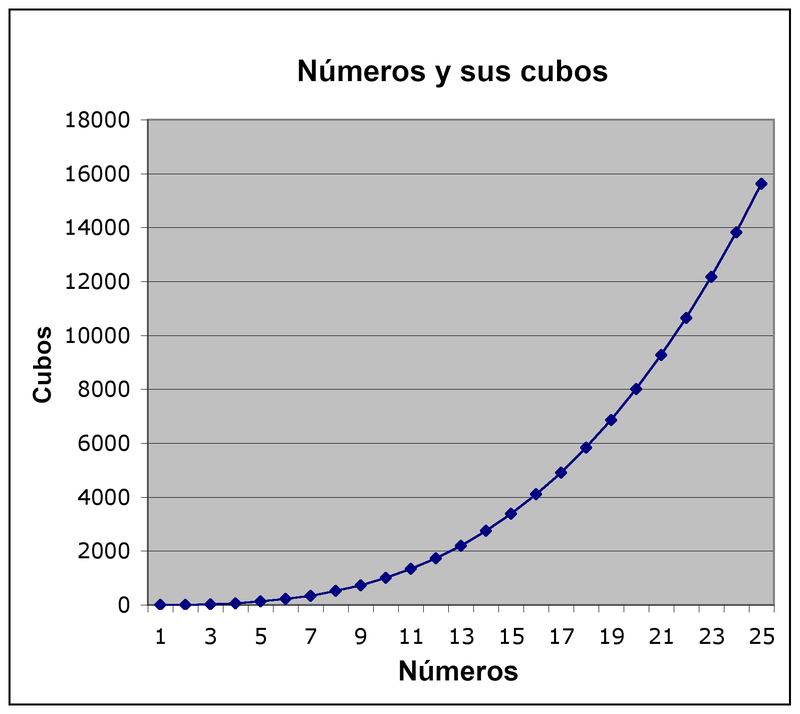
¿Cuántos números del 1 al 1000 son cubos perfectos?
El conjunto de números cubos perfectos es infinito para cualquier número entero (n). Podemos calcular su cubo (n³) y este siempre será un cubo perfecto. No hay un límite superior para los números enteros, los cubos perfectos no tienen una cantidad finita.
- Ejemplo de cubos de los números
- Determinar el rango:
- Queremos los valores de 𝑛 tales que n³≤1000
- Calcular los valores de n:
- 1³ =1 2³ =8 3³ =27 4³ =64 5³ =125 6³ =216 7³ =343 8³ =512 9³ =729 10³ =1000…
- Los cubos perfectos en el rango del 1 al 1000 son:
- 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000
- Hay 10 números cubos perfectos entre 1 y 1000.
- Determinar el rango:
¿Cómo se sacan los cubos perfectos?
Sacar un cubo perfecto consiste en encontrar el resultado de elevar un número entero al exponente 3, calculamos n³ n×n×n. Los cubos perfectos son los números que se obtienen de esta operación. En términos matemáticos, x es un cubo perfecto. Donde se hace la operación con (x= y³) la y es un número entero.
- Pasos para sacar cuadrados perfectos
- Identifica el número: Elige el número entero cuyo cubo quieres calcular.
- Multiplícalo: Realiza la operación de multiplicación del número 3 veces.
- Obtén el resultado: El producto es el cubo perfecto
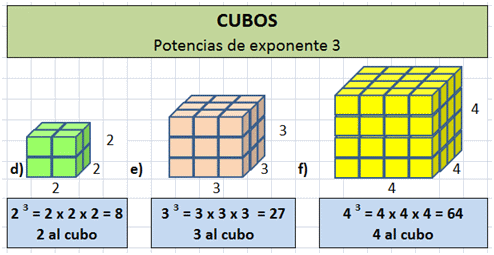
- Ejemplos:
- 1³ = 1 × 1 × 1=1→El cubo perfecto de 1 es 1
- 2³ = 2 × 2× 2=8→El cubo perfecto de 2 es 8
- 3³ = 3 ×3 × 3=27→El cubo perfecto de 3 es 27
- 4³ = 4 × 4 × 4=64. →El cubo perfecto de 4 es 64
- 5³ = 5 × 5 × 5=125→ El cubo perfecto de 5 es 125
- 6³ = 6 × 6 × 6 = 216→ El cubo perfecto de 6 es 216
- 7³ =7 × 7 × 7=343→ El cubo perfecto de 7 es 343
- 8³ = 8 × 8 × 8=512→ El cubo perfecto de 8 es 512
- 9³ = 9 × 9 × 9=729→ El cubo perfecto de 9 es 729
- 10³ = 10 × 10 × 10=1000→ El cubo perfecto de 10 es 1000
- Ejemplos:
La importancia de los números cubos en las matemáticas
Los números cubos, o cubos perfectos, son fundamentales en las matemáticas, con su amplia utilidad y significado teórico. Representan el resultado de elevar un número entero al exponente 3 (𝑛³) y tienen una estrecha relación con el cálculo de volúmenes, que reflejan la estructura tridimensional de un cubo geométrico.
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?
Cargando...
en línea- Relación con las potencias y las raíces
- Comprender el concepto de potencias en un contexto geométrico y algebraico.
- Aplicar raíces cúbicas para descomponer volúmenes y resolver ecuaciones cúbicas.
- Geometría y volumen
- En geometría, los números cubos tienen una conexión directa con el volumen de un cubo tridimensional.
- Aplicaciones en álgebra
- Los números cubos aparecen en la resolución de ecuaciones cúbicas, que tienen importancia tanto teórica y práctica.
- Teoría de números
- Aparecen en ecuaciones diofánticas (el último teorema de Fermat).
- Se relacionan con otras estructuras matemáticas, los números figurados.
- Crecimiento exponencial y patrones
- Los números cubos ayudan a visualizar el crecimiento exponencial en situaciones reales.}
- Ciencias y tecnología
- Física: Los números cubos se utilizan para describir relaciones volumétricas y espaciales.
- Química: En cristalografía, la disposición tridimensional de los átomos sigue principios cúbicos.
- Computación: Los números cúbicos son relevantes en algoritmos de modelado tridimensional y simulaciones.
- Educación matemática
- El estudio de los números cubos:
- Introduce a los estudiantes en conceptos de potencia y raíces.
- Estimula la comprensión del espacio tridimensional.
- Facilita el aprendizaje de temas avanzados, funciones cúbicas y geometría analítica
- El estudio de los números cubos:
- Simbolismo y estructura en matemáticas
- Los números cubos representan el equilibrio tridimensional en matemáticas. Son utilizados, símbolos de estabilidad, crecimiento y complejidad estructural.
La conexión entre números y el universo tridimensional
Los cubos perfectos resultado de elevar un número entero al exponente, representan una unión fascinante entre la abstracción matemática y la realidad tridimensional. Estas potencias no solo permiten calcular volúmenes exactos en geometría, reflejan patrones numéricos que trascienden la aritmética básica. Desde la construcción de modelos espaciales hasta su aplicación en disciplinas, la física y la química, los cubos perfectos son un ejemplo claro de cómo los números pueden describir el mundo que nos rodea.
Los cubos perfectos no son meros cálculos, son una herramienta poderosa para entender las dimensiones, los patrones y la armonía inherente en la naturaleza. Su versatilidad y universalidad demuestran que las matemáticas son mucho más que números; son el puente que une lo abstracto con lo tangible, lo lógico con lo natural.









