En geometría, un cubo es un sólido tridimensional perteneciente a la familia de los poliedros regulares, caracterizado en estar formado con seis caras cuadradas. El cubo es un ejemplo fundamental dentro de los sólidos platónicos, que son figuras geométricas con caras congruentes, aristas iguales y ángulos uniformes. Se encuentra con frecuencia en la naturaleza y en aplicaciones humanas. Desde la estructura molecular de algunos cristales hasta el diseño de objetos cotidianos, dados o cajas

Características generales de un cubo

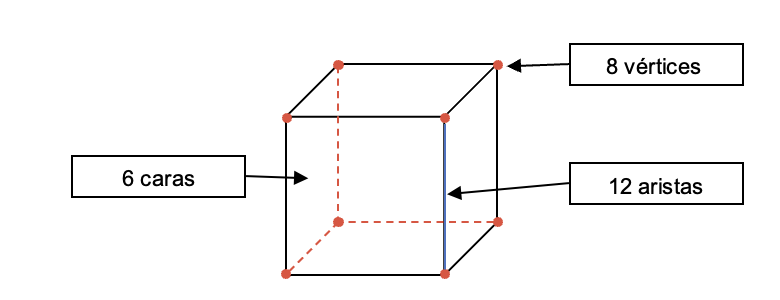
El cubo es un sólido geométrico tridimensional que se define en un poliedro regular con seis caras cuadradas congruentes. Cuenta con 12 aristas de igual longitud y 8 vértices donde se unen tres aristas, formando ángulos rectos en cada intersección. Su estructura simétrica y equilibrada lo convierte en una figura ideal para representar conceptos matemáticos y diseños cotidianos.

• Estructura geométrica
  • Caras: El cubo tiene 6 caras, todas cuadradas y congruentes.
  • Aristas: Posee 12 aristas, que son segmentos de igual longitud.
  • Vértices: Tiene 8 vértices, donde se encuentran tres aristas en cada vértice.
• Simetría y regularidad
  • Es un poliedro regular, todas sus caras y ángulos son iguales. Posee alta simetría, con ejes de simetría, centros de sus caras, aristas y vértices.
• Ángulos
  • Los ángulos entre las caras son siempre ángulos rectos (90°).
  • En cada vértice se encuentran tres ángulos rectos.
• Uso y ejemplos
  • El cubo es una figura ampliamente reconocida en la vida cotidiana (dados, cajas, cubos de Rubik).
  • Es una representación de simetría, equilibrio y estabilidad en geometría y diseño.

¿Cómo calcular el área y volumen de un cubo?

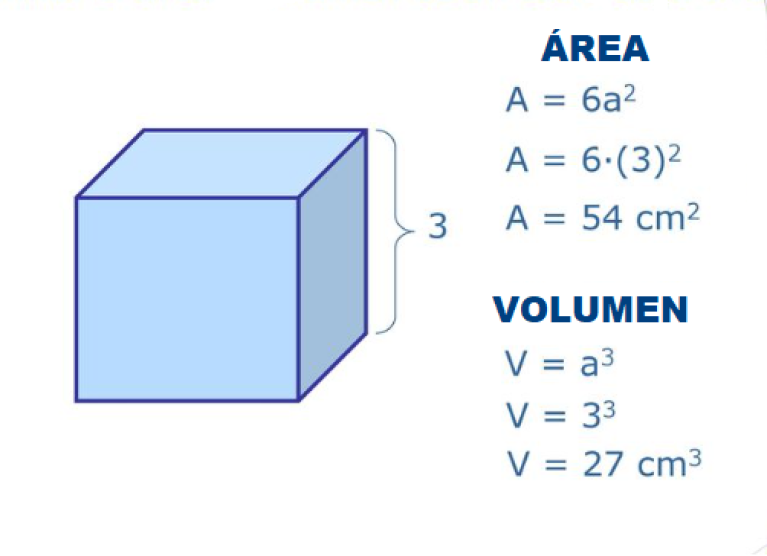
El área de un cubo se calcula multiplicando el área de una de sus caras (x6), un cubo tiene 6 caras iguales. La fórmula para calcular el área de una cara es lado x lado. El volumen de un cubo se calcula con la fórmula (V=a³), donde (a) es la longitud de una de sus aristas. Todas las aristas de un cubo son iguales, no importa cuál se mida. El resultado debe expresarse en unidades cúbicas.

• Área total del cubo
  • El área total de un cubo incluye la suma de las áreas de sus 6 caras cuadradas.
    • Cada cara tiene un área de: Área de una cara=a²
      • Área total=6×a²
• Ejemplo práctico
  • El lado del cubo mide a=5 unidades
    • Área total: Área total=6×5²=6×25=150unidades cuadradas.
    • Volumen: Volumen=5³=125unidades cúbicas.
• Resumen de fórmulas
  • • Área total: A=6×a²
  • • Volumen: V=a³

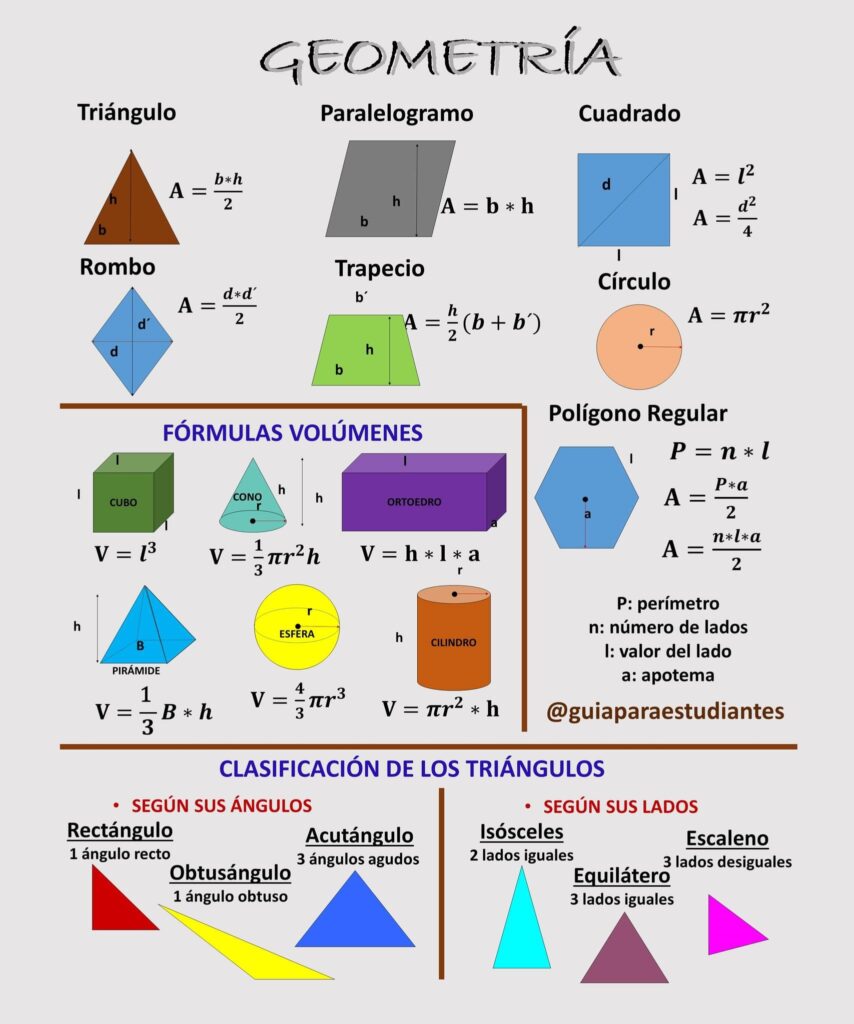
El concepto de geometría en las matemáticas

La geometría es una rama fundamental de las matemáticas que se ocupa del estudio de las formas, las propiedades y las relaciones de puntos, líneas, superficies y cuerpos en el espacio. Surge una necesidad práctica en las primeras civilizaciones para medir tierras, construir estructuras y observar el cielo, con el tiempo, se desarrolló una disciplina abstracta y lógica.

• Principales conceptos de la geometría
  • Punto: Es un elemento básico sin dimensiones (sin longitud, ancho ni altura).
  • Línea: Es una sucesión infinita de puntos en una sola dimensión. Puede ser recta, curva o quebrada.
  • Plano: Es una superficie bidimensional infinita formada con puntos y líneas. En el plano se pueden representar figuras de triángulos, círculos, etc.
  • Espacio: Es el entorno tridimensional donde existen los objetos y los cuerpos geométricos.
• Ramas de la geometría
  • Geometría plana: Estudia figuras en dos dimensiones. Calcular el área de un círculo o un triángulo.
  • Geometría del espacio: Se centra en objetos tridimensionales, cubos, esferas, pirámides y prismas. Determinar el volumen de un cilindro.
  • Geometría analítica: Usa un sistema de coordenadas (el plano cartesiano) para analizar figuras geométricas. Hallar la ecuación de una recta o una parábola.
  • Geometría diferencial: Estudia las curvas y superficies usando el cálculo diferencial y las derivadas.
  • Geometría proyectiva: Se enfoca en las propiedades de las figuras que permanecen invariantes al proyectarlas, en la perspectiva.

El cubo es una figura tridimensional fascinante que combina simplicidad y simetría. Con sus seis caras cuadradas, doce aristas y ocho vértices, representa un ejemplo perfecto de los sólidos geométricos regulares. Comprender sus características no solo nos permite explorar las propiedades del espacio y el volumen, abre la puerta a aplicaciones prácticas en el diseño, la arquitectura y las ciencias.