¿Qué es son los cuadrados y cómo se clasifican?

En geometría, los cuadrados son una figura plana bidimensional con cuatro lados iguales y los cuatro ángulos miden 90 grados. Las propiedades de un rectángulo son similares a las de un cuadrado, la diferencia entre ambos es que en un rectángulo basta con que los lados opuestos sean iguales: todo cuadrado es un rectángulo, pero no todo rectángulo es un cuadrado.

Un cuadrado se puede definir como un rectángulo con dos lados adyacentes de igual longitud. Es el único polígono regular cuyo ángulo interno, ángulo central, y ángulo externo son todos iguales (90°) y cuyas diagonales son todas iguales en longitud. Un cuadrado con vértices ABCD se denotaría ABCD.

Propiedades de los cuadrados#

Los 4 ángulos internos de un cuadrado miden 90º, son ángulos rectos. La suma de los 4 ángulos internos es de 360º. Los 4 ángulos externos miden 90º cada uno y entre los cuatro suman 360º. Las dos diagonales que tienen son iguales y el punto donde se cortan las dos diagonales es el centro de simetría del cuadrado.

• Propiedades de los lados
  • Los cuatro lados son de igual longitud.
    • Los lados opuestos son paralelos.
• Propiedades de los ángulos
  • Todos los ángulos interiores son rectos (90°).
    • La suma de los ángulos interiores es (360°).
• Propiedades de las diagonales
  • Las diagonales son de igual longitud.
    • Las diagonales se bisecan, se cortan en su punto medio.
      • Las diagonales son perpendiculares, formando ángulos de 90°.
      • Cada diagonal divide el cuadrado en dos triángulos rectángulos congruentes.
• Propiedades de la simetría
  • Tiene cuatro ejes de simetría:
    • Dos diagonales y dos que pasan x los puntos medios de lados opuestos.
      • Es simétrico respecto a su centro.
• ​Propiedades relacionadas con el área y el perímetro
  • El área se calcula L² donde L es la longitud de un lado.
    • El perímetro es P = 4 · L.
      • Conocemos la diagonal (d), el área puede expresarse d²/2
• Propiedades de inscripción y circunscripción
  • Un cuadrado puede inscribirse en un círculo y su diagonal será igual al diámetro del círculo.
    • Puede inscribirse un círculo dentro de él, y entonces el radio del círculo es la mitad de la longitud del lado del cuadrado.

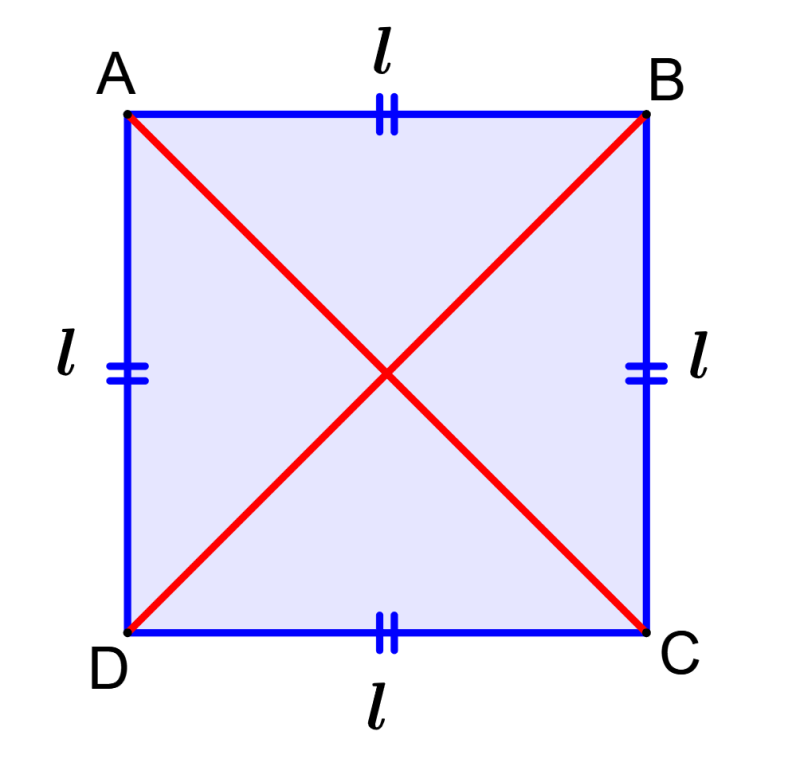
Elementos de los cuadrados#

Los cuadrados son figuras geométricas fundamentales en matemáticas, que forman parte de la categoría de los cuadriláteros. Sus elementos son características específicas que definen su estructura. Estos elementos hacen del cuadrado una figura geométrica con propiedades útiles tanto en geometría en aplicaciones prácticas.

• Lados
  • El cuadrado tiene cuatro lados iguales en longitud.
    • Los lados opuestos son paralelos.
• Ángulos
  • Posee cuatro ángulos internos rectos (de 90° cada uno).
    • La suma de sus ángulos internos es 360°.
• Diagonales
  • El cuadrado tiene dos diagonales que se cruzan en su punto medio.
    • Las diagonales son: Iguales en longitud.
      • Perpendiculares (forman un ángulo de 90°).
      • Bisectrices de los ángulos internos del cuadrado: cada diagonal parte dos ángulos de 90° en cuatro de 45°.
• Centro
  • El centro del cuadrado es el punto donde se cruzan sus diagonales.
    • Es equidistante a todos sus vértices.
• Ejes de simetría
  • Tiene cuatro ejes de simetría:
    • Dos diagonales.
    • Dos rectas que dividen el cuadrado a la mitad, paralelas a sus lados.
• Circunferencia circunscrita
  • Puede trazarse una circunferencia que pasa x todos los vértices del cuadrado.
    • Su centro es el mismo que el del cuadrado, y el radio es igual a la mitad de la diagonal.
• Circunferencia inscrita
  • Puede contenerse una circunferencia dentro del cuadrado, que toca sus cuatro lados.
    • Su centro coincide con el del cuadrado, y el radio es igual a la mitad del lado.
• Lado y perímetro
  • El lado es la longitud de cualquiera de sus lados.
    • El perímetro se calcula sumando todos los lados
• Área
  • El área del cuadrado es el espacio que ocupa y se calcula con la fórmula
    • A = lado²

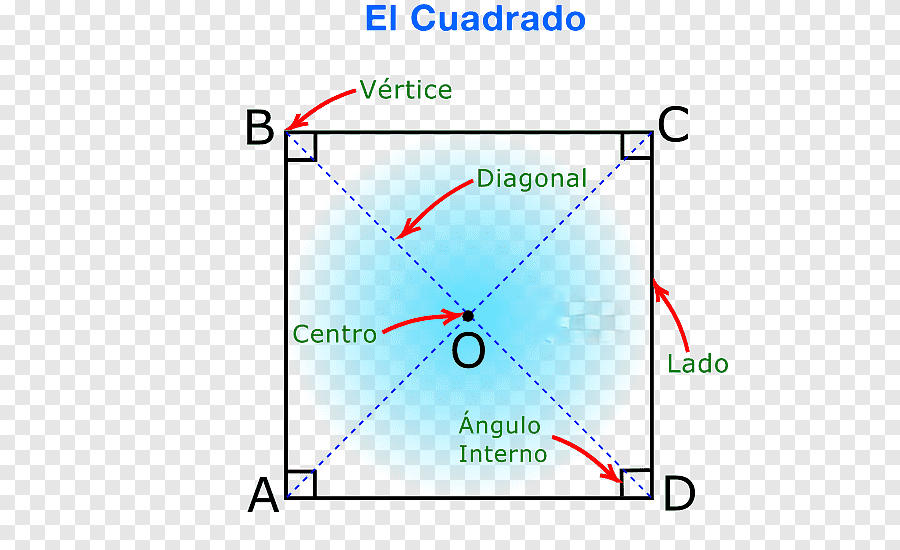
Ángulo interno cuadrado geometría y sus elementos. Cortesía de Wikipedia

¿Qué tipos de cuadrados existen?#

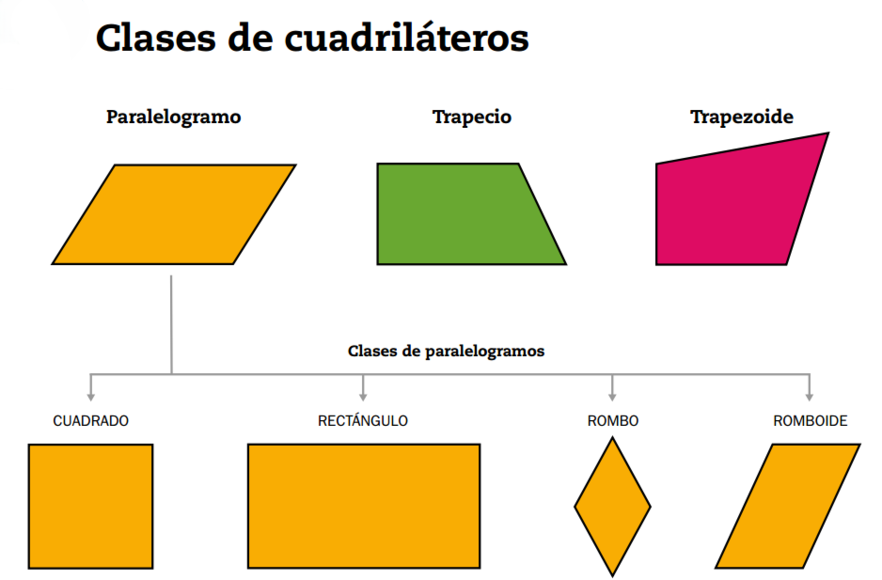
Desde el punto de vista geométrico, todos los cuadrados son iguales, tienen cuatro lados iguales y cuatro ángulos rectos. Pueden clasificarse en tipos según distintos criterios, su posición, relación con otros polígonos o su aplicación práctica.

• Según su orientación
  • Cuadrado “normal” o estándar:
    • Tiene sus lados paralelos a los ejes cartesianos (horizontal y vertical).
• Cuadrado rotado o en posición de rombo:
  • Sigue siendo un cuadrado, se percibe que es un rombo al estar rotado respecto a los ejes cartesianos (una de sus diagonales es vertical u horizontal).
• Según su relación con otros elementos geométricos
  • Cuadrado inscrito:
    • Se encuentra dentro de una circunferencia, todos sus vértices tocan la circunferencia.
  • Cuadrado circunscrito:
    • Es aquel que contiene una circunferencia en su interior, y los lados del cuadrado son tangentes a la circunferencia.
  • Cuadrado asociado:
    • Relacionado con otras figuras geométricas, triángulos, polígonos regulares o sólidos geométricos, sirviendo de base o referencia.
• Según aplicaciones prácticas
  • Cuadrado perfecto:
    • Término usado en álgebra para describir el área exacta de un cuadrado cuyo lado es un número entero.
  • Cuadrado de rejilla:
    • Utilizado en diseño gráfico o sistemas de coordenadas, representando subdivisiones regulares.
  • Cuadrado mágico:
    • Configuración numérica en la que la suma de los números en filas, columnas y diagonales es constante.
• Según sus propiedades algebraicas
  • Cuadrado unitario:
    • Tiene lados de longitud igual a 1 (muy usado en álgebra y geometría analítica).
  • Cuadrado de transformación:
    • Aparece en operaciones de homotecia, rotaciones o reflexiones, con su tamaño o posición modificados.

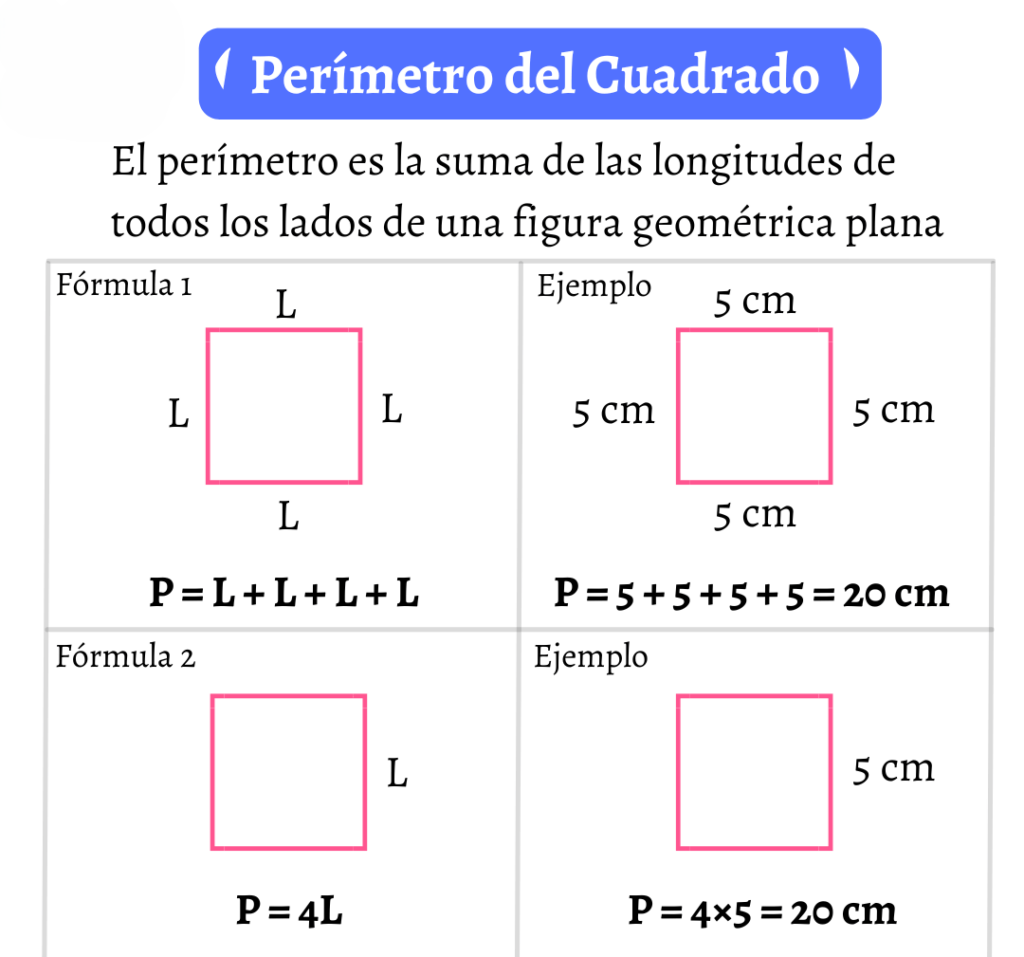
Perímetro#

El perímetro de un cuadrado es la medida de la longitud total de todos sus lados. Tiene cuatro lados iguales, su cálculo es sencillo. Este cálculo del perímetro es útil en problemas geométricos y prácticos, el diseño de cercas o la planificación de bordes en un área cuadrada.

• Fórmula del perímetro:
  • P = 4 ⋅Lado
    • Componentes de la fórmula:
      • P: Representa el perímetro del cuadrado.
      • Lado: La longitud de uno de los lados del cuadrado.
  • Ejemplo práctico:
    • Un cuadrado tiene un lado que mide 5cm, el cálculo del perímetro sería: P = 4⋅5 = 20 cm
• Propiedades relacionadas con el perímetro:
  • El perímetro es una medida lineal y siempre se expresa en las mismas unidades que los lados (metros, centímetros, etc.).
    • El perímetro aumenta proporcionalmente con el tamaño del lado. Duplicas el lado, el perímetro se duplica.

Área#

El área de un cuadrado es la medida de la superficie encerrada dentro de sus lados. Los lados del cuadrado son iguales, su área se calcula elevando al cuadrado la longitud de uno de sus lados. El área del cuadrado es una de las fórmulas más básicas y comunes en la geometría y más prácticas en la vida diaria.

• Fórmula del área:
  • A = Lado²
    • Componentes de la fórmula:
      • A: Representa el área del cuadrado.
      • Lado: La longitud de cualquiera de los lados del cuadrado.
  • Ejemplo práctico:
    • Un cuadrado tiene un lado que mide 6 cm, el cálculo del área sería:
      • A = 6² = 36 cm²
• Propiedades relacionadas con el área:
  • El área es una medida bidimensional y siempre se expresa en unidades cuadradas (cm² m² etc.).
    • El lado de un cuadrado se multiplica x un factor, el área aumenta x el cuadrado de ese factor. Ejemplo duplicas el lado, el área se cuadruplica.
      • Es útil en contextos en el diseño de pisos, planificación de terrenos o cálculos matemáticos más avanzados.

Los cuadrados son figuras geométricas fundamentales con cuatro lados iguales y cuatro ángulos rectos, que se encuentran en diversos contextos matemáticos y prácticos. Su clasificación puede basarse en su posición normales o rotados, relación con otras figuras inscritos o circunscritos y aplicaciones específicas mágicos, unitarios o transformados. Estas propiedades y clasificaciones hacen que los cuadrados sean esenciales para comprender conceptos geométricos, resolver problemas prácticos y explorar conexiones matemáticas más profundas.

Ponte a prueba#

¿Cuánto miden el perímetro y el área de un cuadrado de 5 cm de lado?#

¿Cuánto mide un ángulo externo del cuadrado?#

¿Cuánto mide la diagonal de un cuadrado de 6 cm de lado?#

¿Un cuadrado es un rectángulo?#