Los conos geométricos es un sólido tridimensional con una base circular (o elíptica). Un vértice que no está en el mismo plano que la base. La superficie del cono está formada con todos los segmentos de línea que conectan el vértice con los puntos de la circunferencia de la base. Los conos se considera un círculo y un punto exterior al plano del círculo. La unión de todos los segmentos de extremo en un punto del círculo y extremo común. El punto exterior, se llama cono, considerado un sólido geométrico.
Elementos de los conos
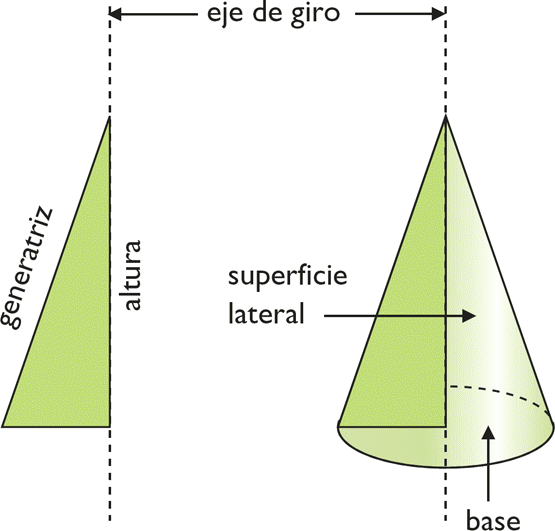
Para visualizar estos elementos, el cono puede dividirse en una base (círculo), una altura perpendicular y una superficie lateral curva que envuelve la figura.
- Base:
- Es un círculo (o elipse) que define el extremo inferior del cono.
- Vértice:
- Es el punto más alto del cono, situado fuera del plano de la base.
- Altura (h):
- Es la distancia perpendicular desde el vértice hasta el centro de la base.
- Generatriz (g):
- Es la línea recta que conecta el vértice con cualquier punto de la circunferencia de la base. Todas las generatrices tienen la misma longitud.
- Eje:
- En un cono recto, es la línea recta que pasa en el vértice y el centro de la base.
¿Qué tipos de conos geométricos existen?
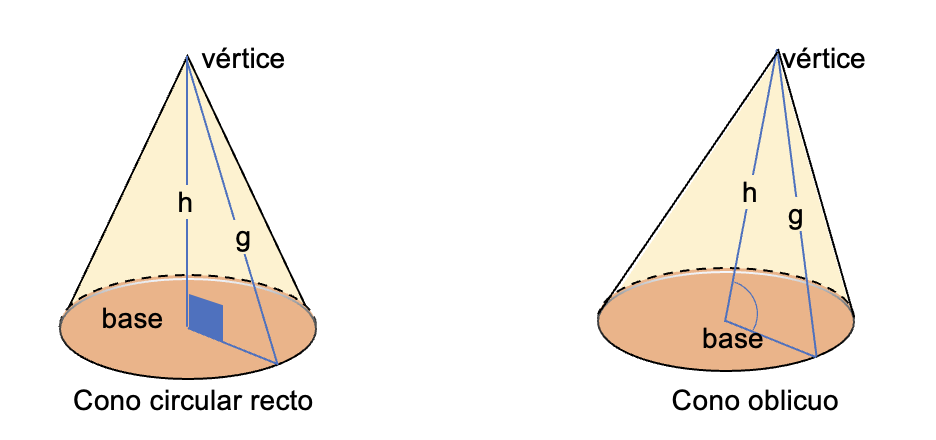
Los conos geométricos se clasifican en rectos y oblicuos. Un cono recto tiene el vértice alineado verticalmente con el centro de su base, formando un eje perpendicular. Su superficie es simétrica, el cono típico que encontramos en matemáticas. Un cono oblicuo el vértice desplazado y no está alineado con el centro de la base.
- Cono recto
- El vértice está directamente alineado con el centro de la base (en perpendicular).
- Su superficie lateral es simétrica y se genera al girar un triángulo rectángulo alrededor de uno de sus catetos.
- Es el tipo más comúnmente estudiado.
- El vértice está directamente alineado con el centro de la base (en perpendicular).
- Cono oblicuo
- El vértice no está alineado con el centro de la base, no forma una perpendicular con la base.
- Su superficie lateral se inclina hacia un lado, dando una apariencia asimétrica.
- Es menos común en aplicaciones básicas, se estudia en geometría avanzada.
- El vértice no está alineado con el centro de la base, no forma una perpendicular con la base.
Área y volumen
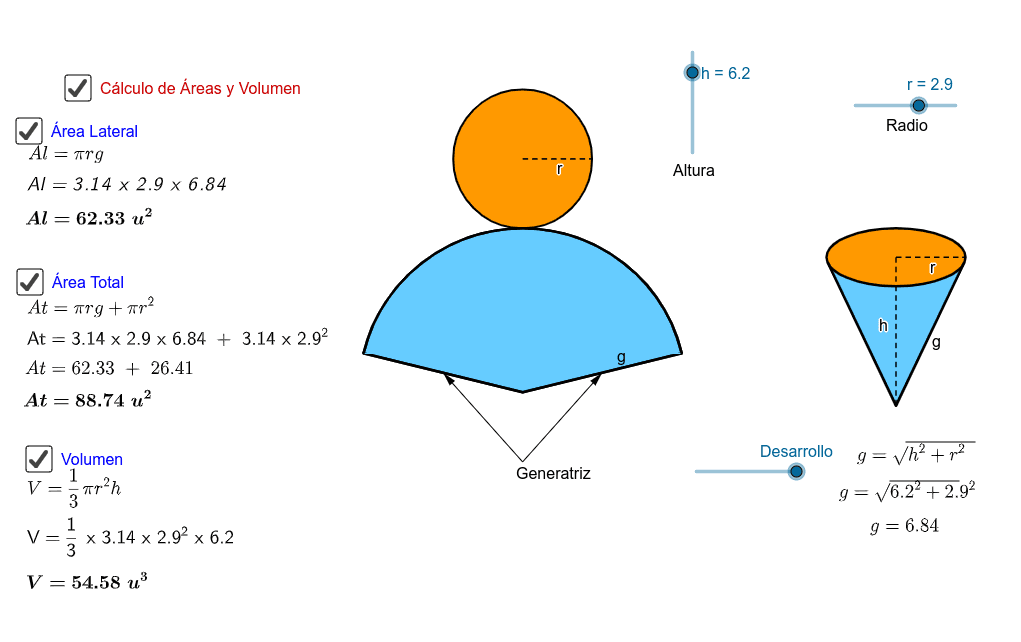
La fórmula que se utiliza para el cálculo del volumen de un cono es: volumen es igual a (π x radio al cuadrado), con la altura entre tres. volumen del cono es igual al área de la base x la altura entre tres.
- Volumen
- El volumen (V) de un cono mide el espacio tridimensional que ocupa y se calcula con la fórmula:
- V=⅓ πr²h Donde:
- r: radio de la base.
- h: altura del cono (la distancia perpendicular desde el vértice al centro de la base).
- π: constante matemática (π ≈ 3.1416)
- V=⅓ πr²h Donde:
- El volumen (V) de un cono mide el espacio tridimensional que ocupa y se calcula con la fórmula:
- Ejemplo:
- El cono tiene un radio de 4 cm y una altura de 9 cm:
- V=3 ⅓π (4)² (9) = ⅓π (144) = 48π ≈ 150.8 cm³
- El cono tiene un radio de 4 cm y una altura de 9 cm:
- Área
- El área total de la superficie de un cono incluye el área lateral (la superficie inclinada) y el área de la base. La fórmula general es:
- Atotal = Alateral + Abase
- Área lateral: Alateral = πrg
- Donde g es la generatriz, que se calcula con el teorema de Pitágoras:
- g = √r² + h² Área de la base: Abase = πr²
- Atotal = πrg + πr² = πr (g + r)
- Atotal = Alateral + Abase
- El área total de la superficie de un cono incluye el área lateral (la superficie inclinada) y el área de la base. La fórmula general es:
- Ejemplo:
- Un cono tiene un radio de 3 cm y una altura de 4 cm:
- Calculamos la generatriz:
- g = √3² + 4² = √ 9 + 16 = √25 = 5
- Calculamos la generatriz:
- Calculamos el área lateral:
- Alateral = π(3) (5) = 15π
- Calculamos el área de la base:
- Abase = π(3)² = 9π
- Un cono tiene un radio de 3 cm y una altura de 4 cm:
- Sumamos para obtener el área total:
- Atotal = 15π + 9π = 24π ≈ 75.4 cm²
La importancia de estas figuras geométricas en matemáticas
El cono es una figura geométrica tridimensional que resulta fundamental en el estudio de las matemáticas y a sus múltiples propiedades y aplicaciones. Compuesta con una base circular y un vértice conectado mediante una superficie curva. Permite abordar conceptos esenciales, el cálculo del área y volumen, es un ejemplo práctico en problemas de geometría. En el cálculo integral. El cono ilustra los volúmenes de sólidos de revolución, ayuda a los estudiantes a comprender el uso de las integrales en contextos tridimensionales.
Chat seguro, privado y nuestro.
¿Te vas a quedar fuera de la conversación?
Cargando...
en líneaLos conos geométricos son figuras esenciales en matemáticas, permite explorar conceptos de área, volumen y sólidos de revolución, fortaleciendo habilidades matemáticas importantes. Su presencia en contextos prácticos, la construcción, el diseño y la naturaleza, refuerza su relevancia en nuestra vida cotidiana. Desde un cono de tráfico hasta la forma de un volcán, esta figura conecta las abstracciones matemáticas con el mundo real, fomentando la creatividad y el pensamiento lógico.









