En matemáticas, la simetría o proporción se refiere a una propiedad en la cual una figura o un objeto se mantiene inalterado. Aplicar ciertas transformaciones, reflexiones, rotaciones, traslaciones o inversiones. La proporción es un concepto clave que se aplica en geometría, álgebra, física y otras áreas de las matemáticas.

La simetría es una de esas nociones que nos resultan más fáciles de intuir que de descubrir o comprender con rigor. Tardamos menos en apreciar las simetrías de las alas de una mariposa que lo que se tarda, en decir que una operación es una transformación matemática, que da lugar a una figura idéntica a la original o una copia especular
de la misma.

Elementos de la simetría

Los elementos de la simetría son componentes clave que describen, la organización y estructura de la misma en figuras geométricas u objetos. Estos elementos permiten identificar y analizar las transformaciones que mantienen inalterada la figura. Se presentan los principales elementos de la misma.

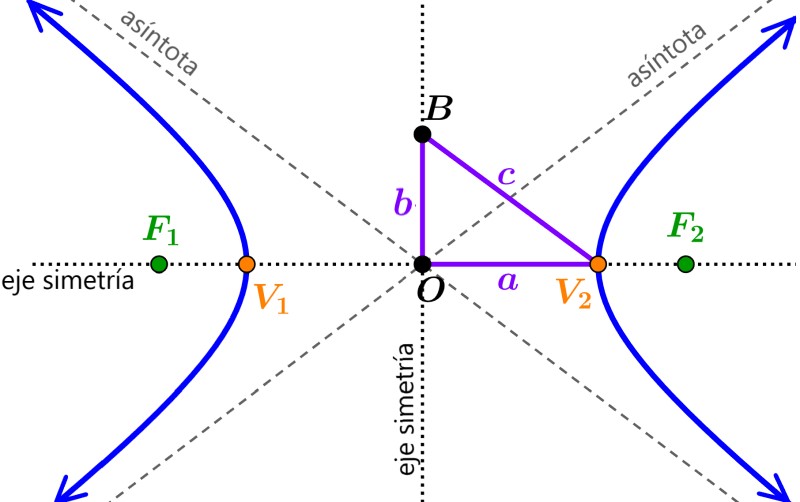
• Eje (o línea)
  • Es una línea imaginaria que divide una figura en dos partes iguales, donde una es el reflejo exacto de la otra.
    • Ejemplo: El eje vertical de una mariposa con las alas abiertas.
      • Puede haber más de un eje de simetría (ejemplo, un círculo tiene infinitos).
• Centro
  • Es un punto en torno al cual una figura puede girar 180° y coincidir exactamente consigo misma.
    • Ejemplo: Un rombo tiene un centro de simetría en el punto donde se cruzan sus diagonales.
• Plano
  • Es un plano imaginario que divide un objeto tridimensional en dos mitades iguales, donde una es el reflejo de la otra.
    • Ejemplo: Una esfera tiene infinitos planos de simetría.
• Ángulo de rotación
  • Es el ángulo mínimo, se debe girar una figura alrededor de un punto (centro de rotación). coincida con su posición original.
    • Ejemplo: Un cuadrado tiene un ángulo de rotación de 90⁰
• Centro de rotación
  • Es el punto fijo alrededor del cual una figura puede girar y coincidir consigo misma.
    • Ejemplo: En un triángulo equilátero, el centro de rotación es el punto de intersección de sus medianas.
• Ejes rotacional
  • En tres dimensiones, son líneas imaginarias alrededor de las cuales un objeto puede rotar un ángulo específico y coincidir con su forma original.
    • Ejemplo: En un cubo, las diagonales que conectan vértices opuestos son ejes de simetría rotacional.

¿Cuáles son los 5 tipos de simetría?

En geometría, los tipos de simetría se refieren a las transformaciones o patrones que mantienen una figura sin cambios en su forma o estructura. Estos tipos son fundamentales para entender patrones en matemáticas, ciencias naturales, arte y arquitectura.

Los 5 tipos principales de proporción son:

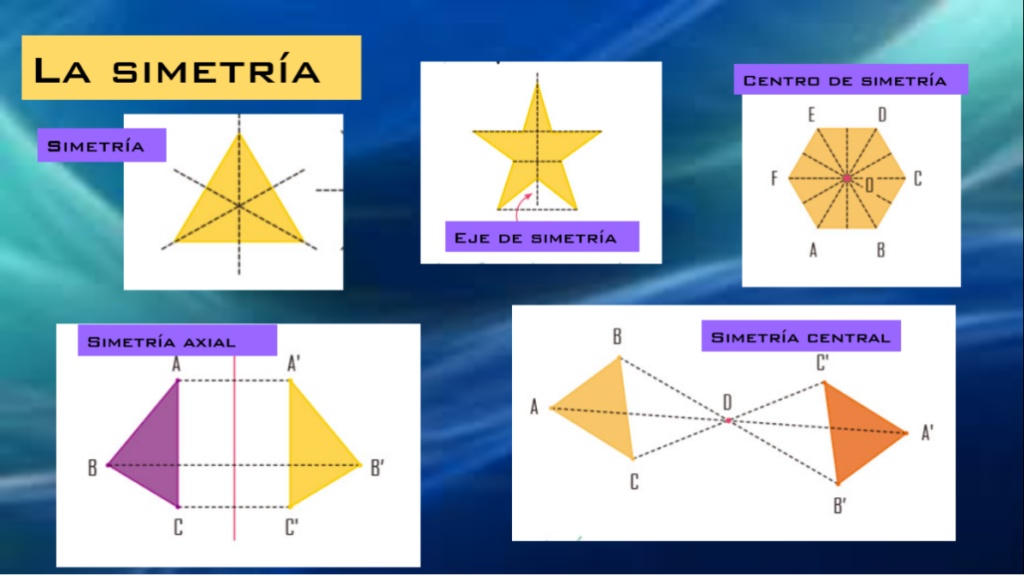
• Proporción de reflexión (especular):
  • La figura puede dividirse en dos partes iguales mediante una línea.
    • Ejemplo: Un corazón partido en dos partes iguales a lo largo de su línea vertical.
• Proporción rotacional:
  • Una figura tiene simetría rotacional y puede girarse (menos de 360°) alrededor de un punto y coincidir consigo misma.
    • Ejemplo: Una hélice de tres aspas tiene simetría rotacional de 120°.
• Proporción traslacional:
  • Una figura se puede trasladar a lo largo de una dirección específica y mantiene su apariencia.
    • Ejemplo: Los patrones repetitivos en papel tapiz o baldosas.
• Proporción Deslizamiento:
  • Es una combinación de simetría traslacional y de reflexión. Una figura es trasladada y reflejada simultáneamente.
    • Ejemplo: Las huellas de animales en la nieve.
• Proporción Central (puntual):
  • Una figura tiene simetría central de cada punto de la figura tiene un punto opuesto a igual distancia de un centro de simetría.
    • Ejemplo: Un rombo respecto a su punto central.

El equilibrio y la armonía en las matemáticas

El equilibrio y la armonía en matemáticas son principios fundamentales que se reflejan en diversos conceptos y aplicaciones. Desde las formas geométricas hasta las funciones algebraicas, el orden y la proporción permiten entender patrones y resolver problemas con mayor eficacia. En geometría, la capacidad de dividir figuras en partes iguales facilita el diseño y la construcción de estructuras. En álgebra, las funciones equilibradas simplifican el análisis gráfico.

• Simetría geometría
  • El concepto clave en geometría, define la forma, proporción y equilibrio en figuras. Existen varios tipos de simetría que pueden explorarse.
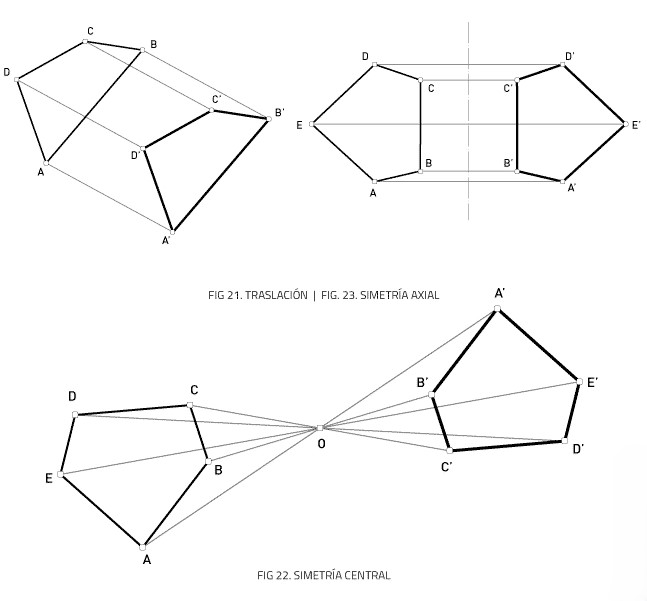
    • Axial o reflejo:
      • Una figura es simétrica, puede dividirse en partes iguales x una línea (eje de simetría). Los triángulos equiláteros y los círculos.
    • Rotacional:
      • Una figura es simétrica, puede rotarse alrededor de un punto y mantenerse igual. Los polígonos regulares.
    • Traslacional:
      • Común en patrones que se repiten, en mosaicos.
  • En álgebra
    • En álgebra, la simetría se manifiesta en las gráficas de funciones matemáticas:
      • Funciones pares: Aquellas cuyos gráficos son simétricos respecto al eje y (y=x²)
      • Funciones impares: Simétricas respecto al origen (y = x³)
    • La simetría facilita la predicción de comportamientos y valores de funciones sin necesidad de calcular todos los puntos.
• Aplicaciones prácticas
  • Arte y diseño:
    • La simetría es un principio estético clave.
  • Ingeniería y arquitectura:
    • Se usa para diseñar estructuras eficientes y estables.
  • Criptografía:
    • Los algoritmos de cifrado a menudo dependen de patrones matemáticos simétricos.

La simetría en matemáticas es mucho más que una propiedad estética; es una herramienta analítica poderosa que conecta diferentes áreas del conocimiento y tiene aplicaciones prácticas en la vida diaria. Su estudio nos permite entender mejor el mundo y resolver problemas de forma más eficiente.