Los cilindros son cuerpos geométricos que se generan al hacer girar un rectángulo alrededor de uno de sus lados. En matemáticas, un cilindro se define con la superficie cilíndrica formada con una recta denominada generatriz. Se desplaza paralelamente en torno a otra recta fija, conocida con el nombre de eje.

La directriz es un círculo y la generatriz se encuentra perpendicular a él. Este movimiento crea una superficie llamada cilindro circular recto, que se considera de revolución y todos sus puntos están a una distancia fija de una línea recta. Llamamos cilindro al sólido delimitado con una superficie y dos planos perpendiculares al eje. Este sólido se utiliza en una superficie Gaussiana.

Elementos de los cilindros geométricos

Los cilindros geométricos son cuerpos tridimensionales que se caracterizan en tener dos bases paralelas y congruentes con forma circular, conectadas en una superficie curva. Este sólido pertenece a la familia de los prismas, se distingue en su sección transversal circular y no de poligonal.

• Bases
  • Son dos superficies planas, congruentes y paralelas.
  • Tienen forma circular (en un cilindro recto) o elíptica (en un cilindro oblicuo).
  • Las bases son fundamentales para determinar el área y el volumen del cilindro.
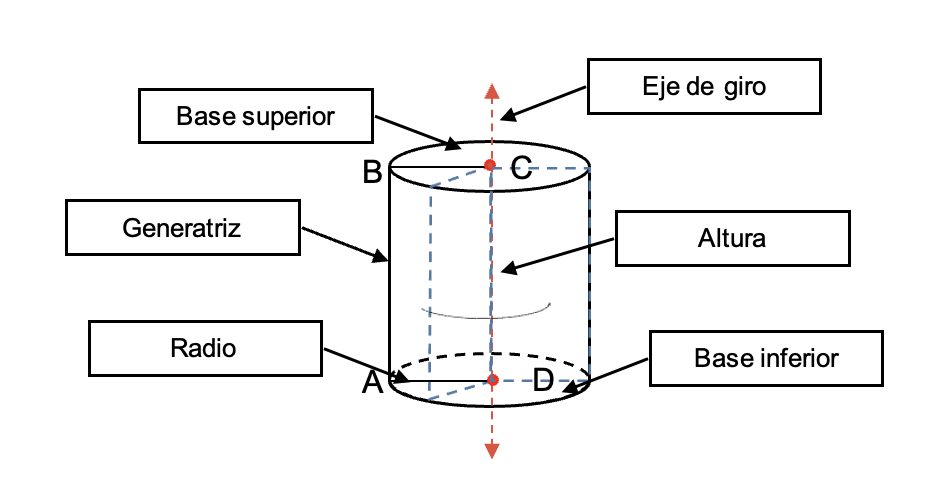
• Altura (h)
  • Es la distancia perpendicular entre las dos bases.
  • En un cilindro recto, la altura coincide con la longitud del eje perpendicular a las bases.
  • En un cilindro oblicuo, la altura es la distancia mínima entre las dos bases, medida de forma perpendicular.
• Generatriz (g)
  • Es un segmento que une dos puntos correspondientes de las bases.
  • En un cilindro recto, la generatriz es perpendicular a las bases y coincide con la altura.
  • En un cilindro oblicuo, la generatriz no es perpendicular a las bases.
• Eje
  • Es el segmento recto que une los centros de las dos bases.
  • En un cilindro recto, el eje es perpendicular a las bases.
  • En un cilindro oblicuo, el eje forma un ángulo con las bases.
• Superficie lateral
  • Es la parte curva del cilindro que conecta las dos bases.
  • Puede imaginarse un rectángulo (se desarrolla sobre un plano) con un lado igual al perímetro de la base y el otro igual a la altura del cilindro.
• Radio (r)
  • Es la distancia desde el centro de una base hasta cualquier punto del borde de esa base.
  • Es un elemento clave para calcular el área y el volumen del cilindro.

Tipos de cilindros

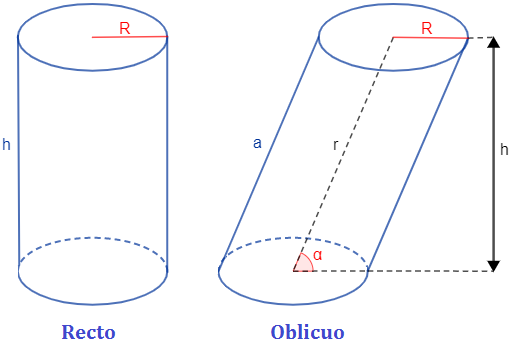
• Cilindro recto:
  • El eje de rotación es perpendicular a las bases. Las bases son círculos, es un cilindro recto circular. El cilindro recto circular puede definirse en un sólido de revolución que se forma de un rectángulo (superficie generatriz Sg) gira 360° sobre uno de sus lados coincidente con el eje de rotación.
• Cilindro oblicuo de base elíptica:
  • El ángulo entre el eje y las bases no es un ángulo recto. La superficie lateral es una superficie cilíndrica de revolución, la sección recta (perpendicular) al eje es un círculo y las bases son elipses.
• Cilindro oblicuo de base circular:
  • El ángulo entre el eje y las bases no es un ángulo recto. La sección recta (perpendicular) al eje es una elipse y las bases son círculos. En este caso, la superficie lateral es una superficie reglada que se denomina superficie cilíndrica de no revolución en la que no existe un eje que equidiste de las posiciones de la generatriz.

¿Cuál es la fórmula de un cilindro?

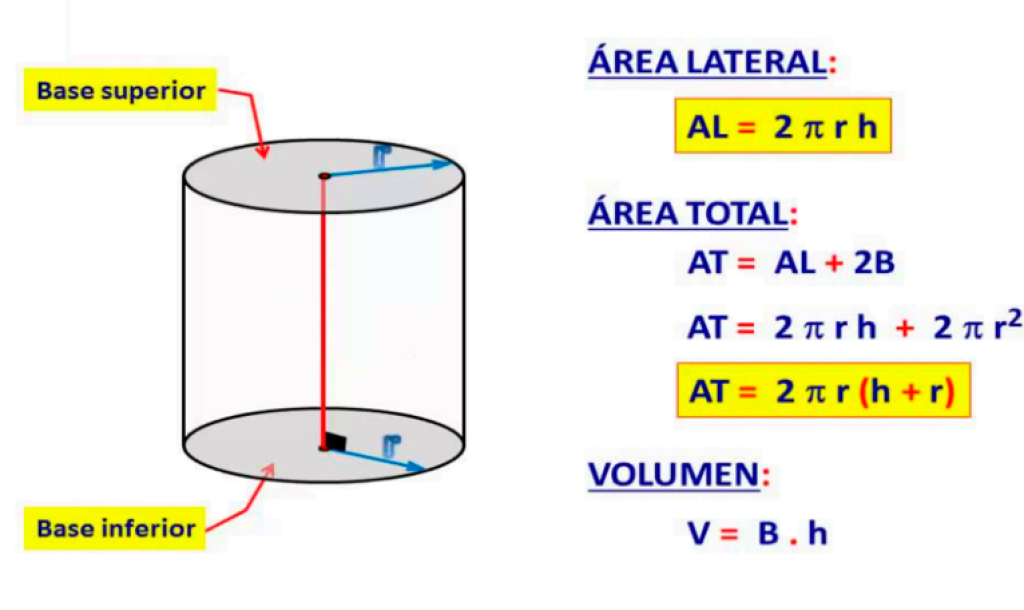
El volumen de un cilindro es π r² h, y el área de su superficie es 2π r h + 2π r². Aprende a utilizar estas fórmulas para resolver un problema de ejemplo.

• Área de la base (círculo)
  • La base del cilindro es un círculo. Su área se calcula:
    • Abase​=πr² Donde: r es el radio del círculo.
• Área lateral
  • El área lateral es la superficie alrededor del cilindro sin incluir las bases. Se calcula
    • Alateral​=2πrh. Donde: r es el radio. h es la altura del cilindro.
• Ejemplo: Calcular el área lateral de un cilindro
  • Problema: Un cilindro tiene un radio de 4 cm y una altura de 12 cm.
    • Solución: Usamos la fórmula del área lateral: 𝐴lateral 2𝜋𝑟ℎ
      • Sustituyendo: Alateral=2π(4)(12) =2π(48)=96π
      • El área lateral es: ≈301.59cm² (usamos π≈3.1416)
  • Valor de π es de 3.1416
• Ejemplo: Calcular el volumen de un cilindro
  • Problema: Un cilindro tiene un radio de 5 cm y una altura de 10 cm.
    • Solución: Usamos la fórmula del volumen: V=πr²h
      • Sustituyendo: V=π(5)²(10)=π(25)(10)=250π
      • El volumen es: V≈785.4cm³(usamos π≈3.1416)
  • Valor de π es de 3.1416

La importancia de estas figuras geométricas

Los cilindros tienen una gran importancia tanto en el ámbito práctico, en el teórico sus propiedades geométricas y aplicaciones en la vida cotidiana. En la ingeniería y la arquitectura, su forma proporciona estabilidad estructural, lo que los hace ideales para construir columnas, tuberías y recipientes de almacenamiento. El diseño industrial, los cilindros se utilizan en motores, pistones y ruedas, componentes clave para el funcionamiento de máquinas y vehículos.

En matemáticas, el cilindro es una figura esencial para estudiar conceptos de volumen, área y secciones transversales, lo que contribuye al desarrollo de la geometría y el cálculo. Su presencia en la naturaleza y en fenómenos físicos, las corrientes de agua y los flujos de aire, lo convierte en un modelo ideal para el análisis y resolución de problemas científicos. En conjunto, los cilindros son indispensables en múltiples campos del conocimiento y la tecnología.