La suma de fracciones es una operación fundamental en matemáticas que permite combinar dos o más en una sola. Para realizar esta operación. Debemos considerar las fracciones tienen el mismo denominador (fracciones homogéneas) o diferentes denominadores (fracciones heterogéneas). El procedimiento varía en cada caso.
El proceso de sumar fracciones involucra la comprensión de los conceptos de numerador, denominador y el uso del mínimo común múltiplo. En el caso de una fraccion heterogéneas. Esto hace de la adición de una fraccion una habilidad clave en la aritmética. Un paso importante en el aprendizaje de operaciones más avanzadas con fracciones y números racionales.
Numerador y denominador en la suma fracciones
En la suma de fracciones, el numerador y el denominador cumplen roles importantes. El numerador, que está en la parte superior de la fracción, indica la cantidad de partes que se toman en cuenta. El denominador, ubicado en la parte inferior, muestra en cuántas partes se ha dividido el todo.
Las fracciones que tienen denominadores distintos, se dice que es una fracción heterogénea. Para sumarlas, es necesario convertirlas en fracción con el mismo denominador. Para ello, encontramos el mínimo común múltiplo (MCM) de los denominadores y convertimos cada fracción a un denominador común.
- El numerador:
- Se suma y se obtiene la cantidad total de partes en las fracciones, con un denominador común.
- El denominador:
- Establece en cuántas partes se divide la unidad y, en caso de fracciones heterogéneas, se iguala mediante el mínimo común múltiplo para permitir la suma.
- Ejempló: 2/7+3/7
- Aquí, solo los numeradores (2 y 3) se suman, el denominador (7) permanece igual.
- 2+3=5 la fracción seria 5/7
- Aquí, solo los numeradores (2 y 3) se suman, el denominador (7) permanece igual.
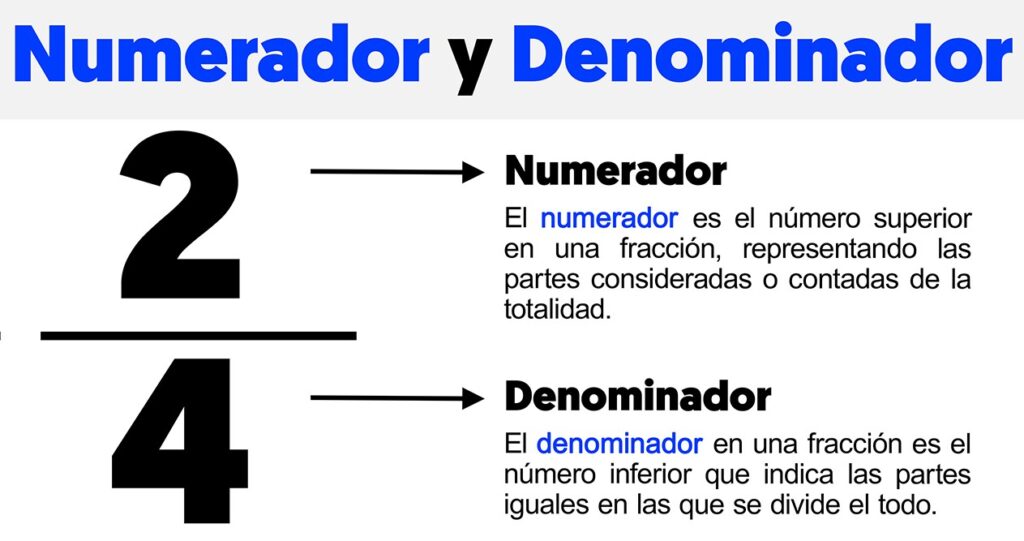
¿Cómo es la suma de fracciones con el mismo denominador?
Para resolver una suma de una fracción, es importante identificar si las fracciones son homogéneas o heterogéneas. Si las fracciones tienen el mismo denominador (homogéneas), el procedimiento es sencillo: solo se suman los numeradores y se mantiene el mismo denominador.
Para resolver una adición de fracciones, primero es esencial asegurarse de que las fracciones involucradas tengan un denominador común. Si no lo tienen, es necesario calcular el mínimo común múltiplo (MCM) de los denominadores. Este proceso garantiza que los valores se puedan sumar correctamente, al tener el mismo denominador permite sumar directamente los numeradores de cada fracción.
- Suma de fracciones con el mismo denominador
- Se suman los numeradores.
- Se deja el mismo denominador.
- Se suman los numeradores.
- Ejemplo 1: 3/8 + 2/8
- Sume los numeradores 3 + 3= 5 la fracción seria 5/8
- Se deja el mismo denominador
- Sume los numeradores 3 + 3= 5 la fracción seria 5/8
- Ejemplo : 2/5 + 1/5
- Sume los numeradores 2 + 1= 3 la fracción seria 3/5
- Se deja el mismo denominador
- Sume los numeradores 2 + 1= 3 la fracción seria 3/5
- Ejemplo 3: 3/10 +4/10
- Sume los numeradores 3 + 4= 7 la fracción seria 7/10
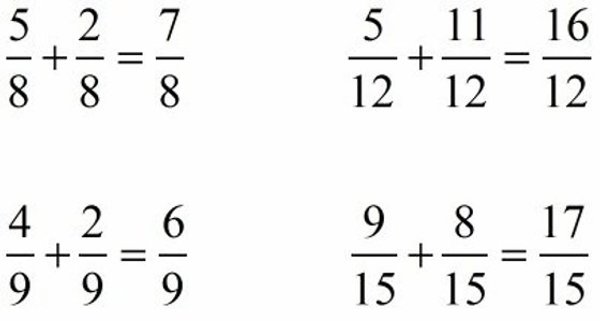
¿Cómo es la suma de fracciones con diferente denominador?
La suma de números racionales con denominadores diferentes requiere un procedimiento que iguale sus denominadores. Para lograrlo, se encuentra el mínimo común múltiplo (MCM) de los denominadores, lo que permite convertir cada número racional a una forma equivalente con el mismo denominador.
El resultado final, que representa la suma de los números racionales en una expresión unificada, puede requerir simplificación. Este método es fundamental en las matemáticas, (álgebra), facilita operaciones básicas y es un paso clave en la resolución de ecuaciones racionales.
- Adición de una fracción con diferente denominador
- Se encuentra el mínimo común múltiplo (MCM) de los denominadores, que será el denominador común.
- Se convierten ambas en equivalentes que tengan el denominador común.
- Se suman los numeradores.
- Ejemplo: 2/5 + 3/7
- Paso 1: El MCM de 5 y 7 es 35.
- Paso 2: Convertimos ambas fracciones:
- 2/5: multiplicamos tanto el numerador y denominador (x 7), lo que da:
- 2 × 7= 14 y 5 × 7= 35 resultado 14/35
- 3/7: multiplicamos tanto el numerador y denominador (x 5), lo que da:
- 3 x 5= 15 y 5 x 7= 35 resultado 15/35
- 2/5: multiplicamos tanto el numerador y denominador (x 7), lo que da:
- Paso 3:
- Ahora que ambas fracciones tienen el mismo denominador, podemos sumar los numeradores:
- 14 + 15= 29 y denominador que igual 35
- Resultado: La suma de fracciones 2/5 y 3/7 es 29/35
- 14 + 15= 29 y denominador que igual 35
- Ahora que ambas fracciones tienen el mismo denominador, podemos sumar los numeradores:
El fascinante mundo de los conceptos matemáticos
El mundo de los conceptos matemáticos es un vasto universo de ideas que muchas veces pasan desapercibidas, sostienen gran parte de la realidad que vivimos y experimentamos. Desde los fundamentos de la aritmética hasta los sistemas complejos de álgebra y cálculo, cada concepto matemático tiene un propósito y una belleza única, revelando patrones, relaciones y reglas que dan sentido al mundo que nos rodea.
Cada rama de la matemática, las fracciones, la geometría, la estadística o la probabilidad, que abordan preguntas fundamentales y nos permite interpretar fenómenos en campos de la física, la economía y la informática. Al comprender estos conceptos, nos damos cuenta de que las matemáticas no son solo números o fórmulas abstractas, es un lenguaje universal que describe desde los más pequeños elementos hasta el funcionamiento del cosmos.
La suma de fracciones es un paso importante en el aprendizaje matemático, nos ayuda a comprender cómo combinar partes para formar un todo. Parece complicado sumar fracciones, en otra medida se convierte en una herramienta versátil y útil. Este conocimiento no solo es esencial en el aula y tiene aplicaciones prácticas en la vida cotidiana. La matemática, la suma de fracciones, nos enseña a resolver problemas de manera ordenada y lógica descubriendo cada concepto matemático abriendo una puerta de nuevas habilidades y desafíos.
